大学的部分考试采用了这样的一种半开卷模式,即允许携带一张A4纸大小的Cheatsheet,但不允许携带任何其它参考资料。此时,这一张Cheatsheet对于同学们,尤其是缺乏复习准备的同学们来说,极有可能是决定成绩的肯綮。在本文中,我试图通过展示最近离散数学考试Cheatsheet的制作流程,探究制作Cheatsheet的基本思路。
选择合适的工作流
首先,我们需要分析Cheatsheet制作过程中的主要矛盾。Cheatsheet,究其形式,本质就是含有大量知识点的资料。但是,教材、讲义本质上也是这样的资料。那么,Cheatsheet到底有什么特别之处,值得我们深究呢?以下我总结了三个特点。
首先是“急”。大学课程十分紧张,往往考试范围正是已学内容。因此,我们不可能具备充裕的时间准备Cheatsheet。此外,Cheatsheet是为了辅助一场考试的,而不是装裱起来供人膜拜的,如果将过多的时间投入到Cheatsheet制作中,反误了复习,必得不偿失。因此,Cheatsheet工作流应当做到“快速”(Fast)。

其次是“限”。使用Cheatsheet的考试之所以能被冠以“半开卷”之名,正是因为它所能承载的内容实在是过分有限。如果不经过有技巧性的设计,很难在一张A4纸上承载所有重要的知识点。而同时,在编纂Cheatsheet时,我们很难估计会写下多少内容,从而无法估计在何种设计下能够让一张纸承载所有文字。因此,我们应当能够很方便地调整版面、字体、段落等设计,Cheatsheet工作流应当做到这样的“灵活”(Flexible)。

最后是“慌”。考试时,常会有无法预估的情况出现,譬如题目过难、过多等。此时我们很容易出现“慌张”的情况。在这种状态下,我们先前设计的各种“暗号”“简称”“编码”等都有可能被完全忘掉,使得我们在看Cheatsheet时四顾而茫然,以至于证明题中某一个条件没写出来,从而与A+失之交臂。所以Cheatsheet中,所有内容都应当以能够直接在考试中照抄到试卷上的格式写出。这也就是Cheatsheet工作流所需的“一致”(Consistent)。
以上,我们分析了Cheatsheet应当做到的三个要求:快速、灵活、一致。基于这三个要求,我们对以下常用工作流进行分析:
| 序号 | 内容编写 | 排版 | 交付 |
|---|---|---|---|
| 1 | 手写 | 凭感觉设计 | 手写 |
| 2 | 任意编辑器 | 凭感觉设计 | 手写 |
| 3 | 记事本 | 记事本 | 打印 |
| 4 | Word | Word | 打印 |
| 5 | LaTeX | LaTeX | 打印 |
| 6 | Markdown | Markdown编辑器 | 打印 |
考虑到“快速”,显然方案1和方案2的手写是应当被排除的。手写不仅誊写缓慢,如果出现较大范围的改动,便只能重新誊抄,花费大量时间。
考虑到“灵活”,则方案4的Word方案应当被排除。虽然Word功能强大,且被广泛使用,但在包含公式的情况下,精密排版便成为了奢望。如果没有丰富的排版经验和足够的微调时间,抑或是出现了大范围改动,将会出现一场“灾难”。从另一方面来说,这也违背了“快速”原则。
考虑到“一致”,方案3的纯记事本方案也得被排除。这个方案并不能直观地显示公式。
此时还剩下LaTeX方案和Markdown方案。对于善于使用LaTeX的同学,LaTeX是可以使用的。但是,相比Markdown,LaTeX在配置方面需要更多工作,因此没那么“快速”;同时,其过于强大的排版功能反而也可能导致在更改排版时没那么“灵活”。因此,在这次离散数学Cheatsheet制作中,我采用了Markdown工作流。

正确地组织内容
对内容进行正确的组织,不仅可以简化编写流程,还可以在考试时提高索引效率。在离散数学Cheatsheet设计中,我的方法是将定义、定理分成两个板块;在每个板块中,又根据授课顺序,将内容分为多个单元,其中每个单元对应一节课的授课内容。至于版面设计,我采用了长竖版拼接的方案,也就是将内容生成在较窄的竖条形空间内,再将空间截断,横向拼接。以下,我将继续从“急”“限”“慌”三个问题分析这种内容组织方式的合理性。
首先,我将定义、定理明确分成两个板块。乍一看,这增加了内容撰写花费的时间,似乎不适应“急”这一特点。然而实际上,在Cheatsheet制作中,我发现定义和定理的结构是存在较大区别的。一般而言,定义的基本结构是“某事物是如何如何的什么”,而定理的结构则较为多变,包括“如果如何如何则如何如何”“任意什么都有如何”等。如果将定义、定理放在一起,尤其在换行的部分,容易显得不整齐,导致在查找时需要花费更多心思,反而降低了索引的效率,不适应“慌”这一特点。那么,Cheatsheet制作中,我们应当优先考虑“急”还是“慌”呢?很显然,应当是“慌”。Cheatsheet是为了考试服务的,一切设计思路的核心都是为了考试时方便,因此,考试时出现的“慌”的问题理所应当地成为了主要矛盾。因此,此时的“急”作为次要矛盾,反而可以让步。
实践中,这两点并非枘凿。我们应当记住,文档编写虽然整体上是线性的,但不意味着我们只能从头到尾编写。在我的方案中,只有两个板块,那么就可以同时打开这两个板块的编辑器,同时进行编写。如此,“急”的问题也得到了解决。
顺序编排,尤其是定义的顺序编排,也是集中于解决“慌”的问题。我考虑过两种编排方式,其一为按拼音字母顺序编排。这种方式被广泛地应用在各种中文资料的索引中,是约定俗成的“理想”方法。然而,对于Cheatsheet而言,依然“理想”吗?我们应当思考,为何它能成为“默认”的编排顺序。对于大多数资料索引而言,其面向的对象大多是并未对资料有足够多的理解,而又希望能够快速地查找到所需内容的使用者。而拼音字母序编排基于公众普遍掌握的中文拼音规则和拉丁字母表顺序,是一个理想的“先验假设”。对于这类资料而言,拼音字母顺序编排能够最大化使用者的期望查找效率。
但是,对于Cheatsheet而言,这一假设过于弱了。考试并不是即兴资料分析,而是在大量授课的基础上进行的教学质量检测。每一位正常参与课程的同学,都应当对课程的基本结构有一定的了解,同时也能够根据授课顺序,对各种内容形成一种思想上的关联。在这种情况下,按照知识板块进行排序,反而是更加自然,更加理想的方式。正因此,我选用了第二种编排方式,即按授课顺序分单元编排。
版面设计的方案则用以在“限”和“慌”进行平衡。我们能够注意到,这两个条件的本质有很大区别。“慌”是渐进的,随着我们排版的“可索引性”下降,“慌”的矛盾是逐渐变得突出。然而“限”是离散的,一旦我们的设计方案无法使我们在一张A4纸内,以打印机能清晰印刷的字体包含所有内容,我们就只能面临丢弃部分内容或使所有内容都模糊不清的两难困境——而内容模糊不清,更是直接将“慌”推向了极致。所以,排版方案应该在绝对确保“限”的条件能够被满足的情况下,尽可能地解决“慌”的问题。
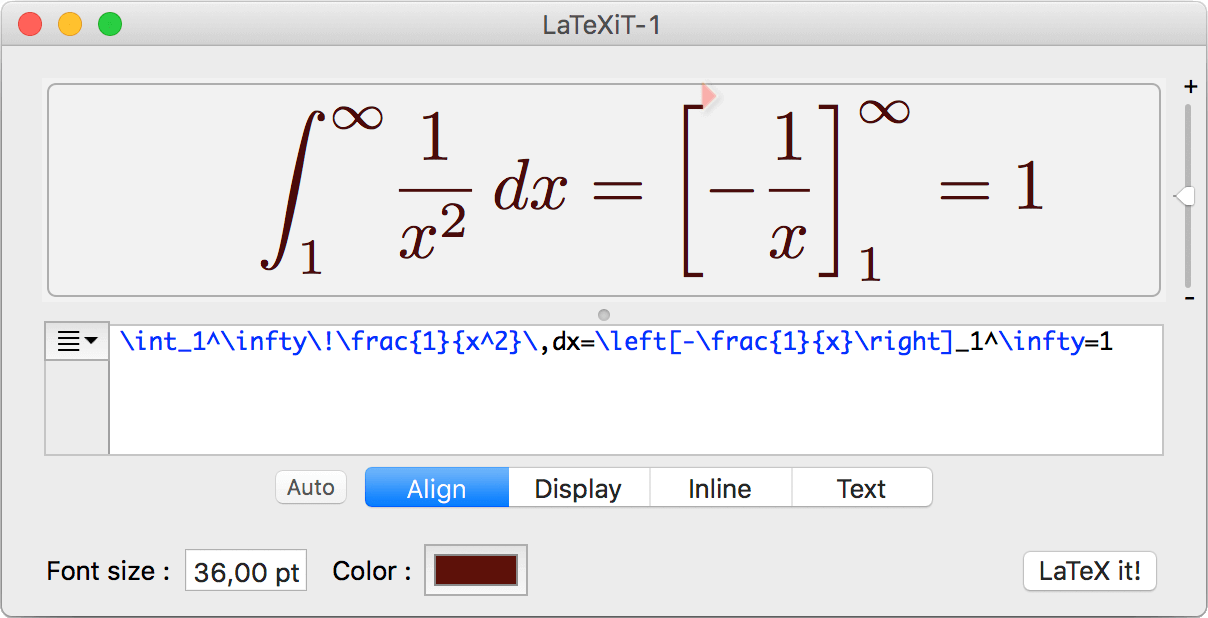
在有限的空间内写入尽可能多的内容,而又不至于使文字太小,就需要从“开源”和“节流”两方面解决。首先是“开源”,也就是想方设法从边边角角找到能够增加内容的地方。我采用的策略是将边距全部设置为零,同时采用横版编排。通过将边距设为零,可以将原本是空白的页眉、页脚、页边使用上。而横版编排使得在考试中人眼到纸张的平均距离更近,文字在人眼中占据的角面积更大,从而能够使在保持相同分辨效果的情况下,字体可以小一点。其次是“节流”,也就是尽可能避免浪费空间。这次离散数学Cheatsheet编排中,我发现主要导致浪费空间的地方在两处,一处是每行定义、定理末尾换行后的留白,另一处是部分高度较大的数学公式导致过大的行间距,从而导致的留白。解决第一种浪费的方法是尽可能采用较窄的编排宽度。但前文提到,要“开源”,得横版,这就产生了矛盾。我解决这个矛盾的方法是,将内容分列显示。经过测试,A4纸分拆成6列的效果能够较好地平衡观感和内容密度。解决第二种浪费的方法是尽可能将公式横向化,譬如使用\sum_{i=1}^n而不是\sum\limits_{i=1}^n,使用(x+1)^{-1}而不是\frac{1}{x+1}。
简要的编写流程
以上两部分,我阐述了Cheatsheet的基本编写思想。以下我简单地展示一下本次离散数学Cheatsheet的编写流程。
首先,使用支持LaTeX公式的Markdown编辑器编纂内容。市面上有很多这类编辑器,如MarkText、Typora等。此外,VSCode也是不错的选择,但需要注意的是,VSCode导出内容并不太方便。

然后,导出长竖条版式的内容。这里建议将字号调大,同时将页面调大,以生成更加清晰的文档。注意此处要将页边距全部调为零,且页面大小应当为99mm x 420mm的倍数。
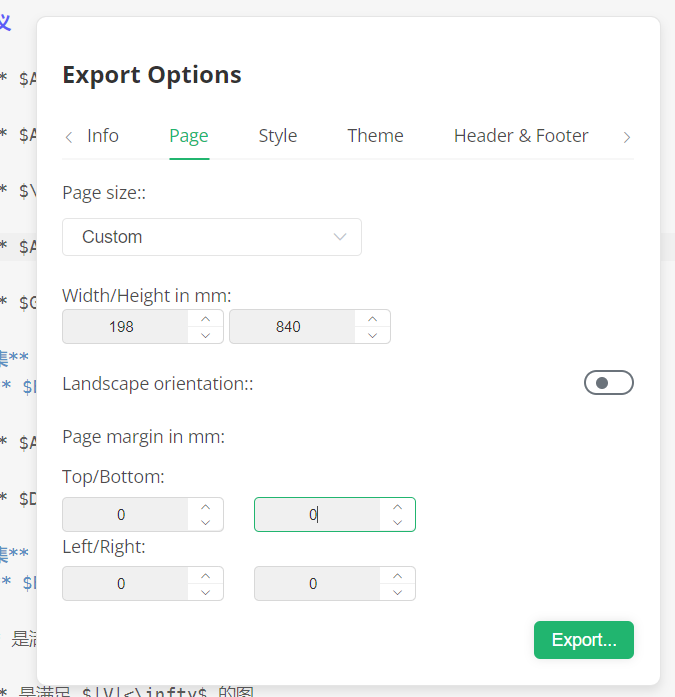
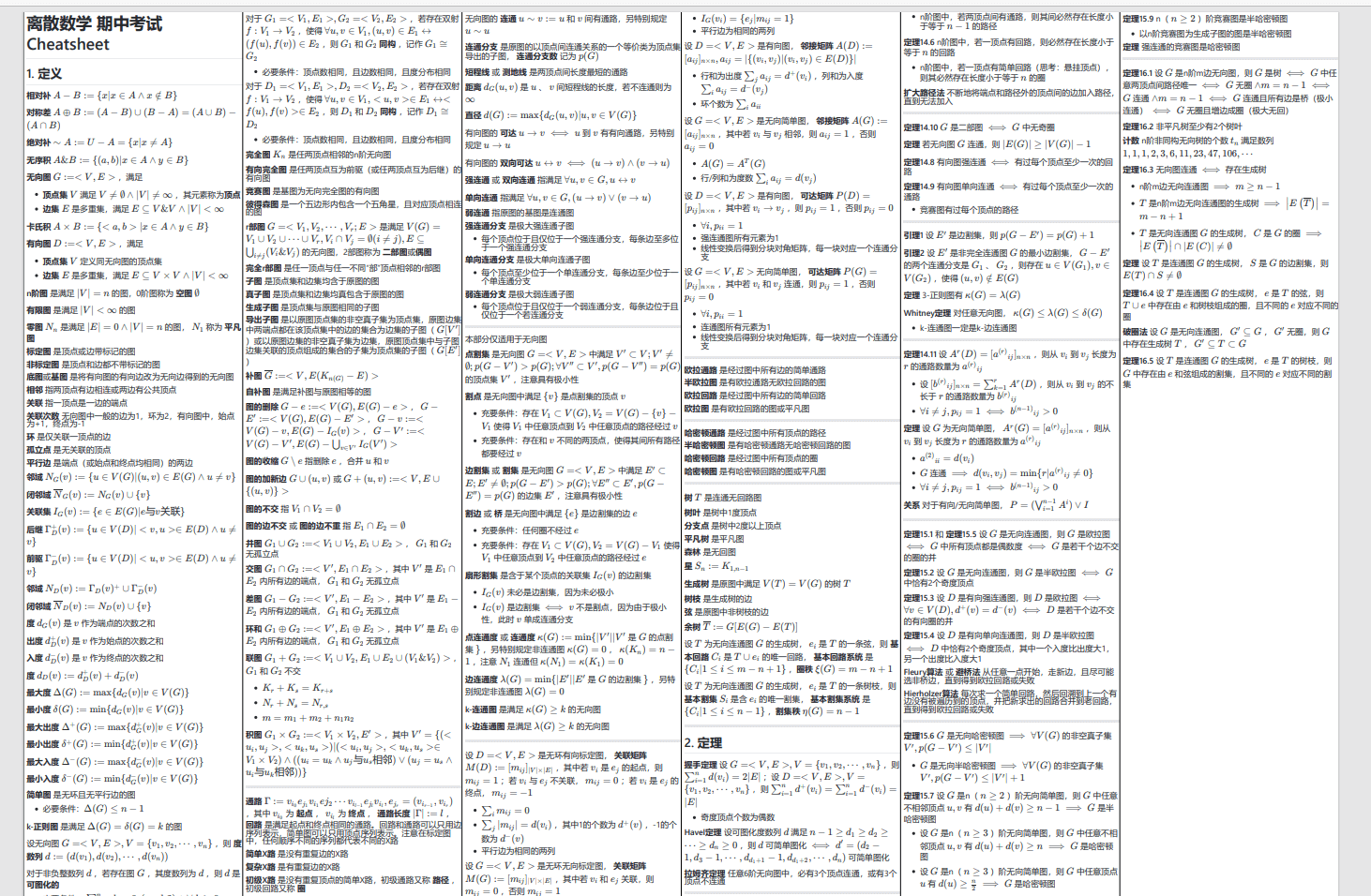
将导出的内容通过拼接工具(网络上很多在线工具)进行横向拼接,就可以得到一个和A4纸比例一致的文档。
最后,也是比较重要的一步,就是需要稍微调小一点页面内容范围,否则打印机可能无法正确打印。我们可以使用Windows系统自带的Print to PDF功能。
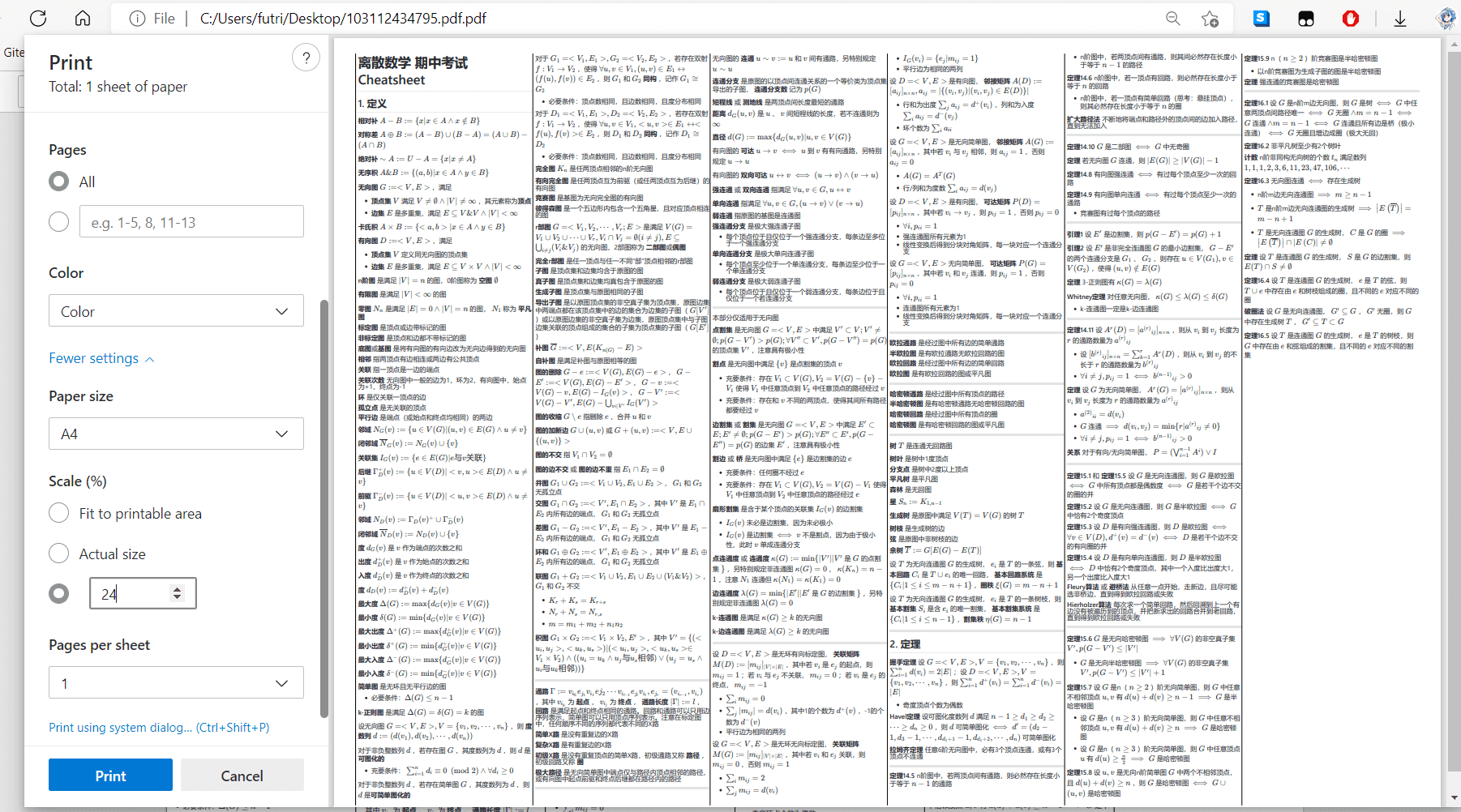
随后打印即可。
